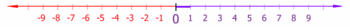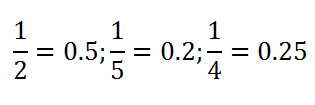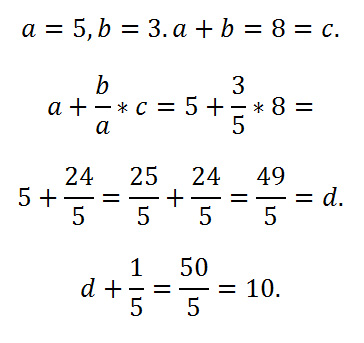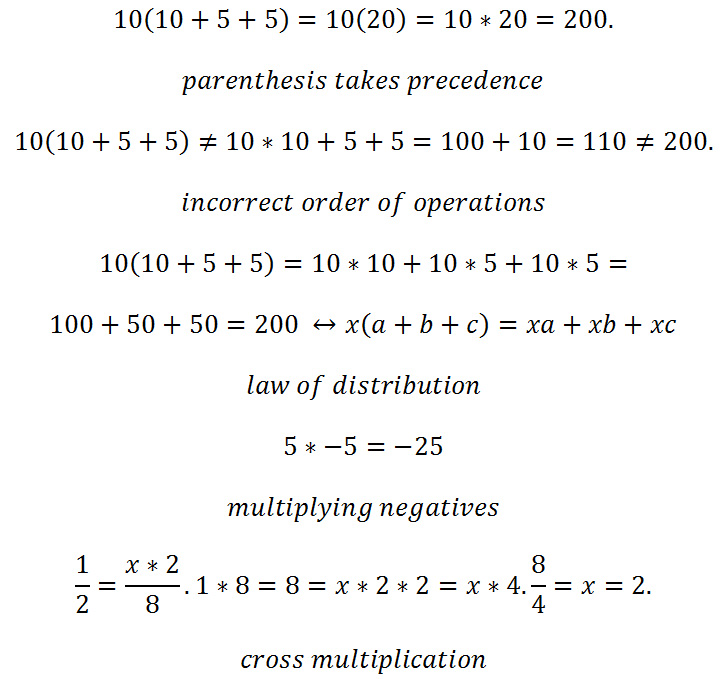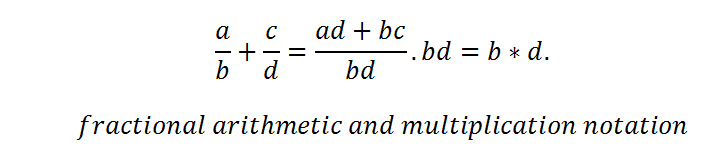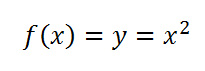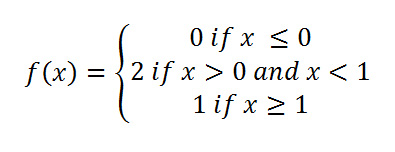Geometry

Contemporary geometry concerns 2d and 3d structures, and is fundamentally important to understand. Geometry relies on some basic algebraic principles, which will also be covered here. For computer graphics, geometry can be used to define primitive shapes.

The most important types of numbers with respect to digital art are integers and decimal numbers (fractions):

integers on a number line, always being displayed as whole numbers with no decimal indication. they can be positive or negative with respect to 0

mathematical truths with fractions on left of the equals sign and decimals on right

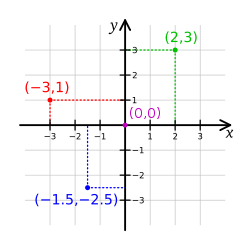
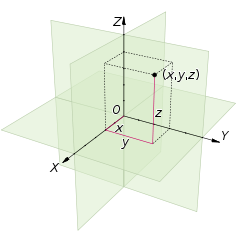
All geometry is based on the cartesian coordinate system, which defines points in space based on axes and an origin located at the center:

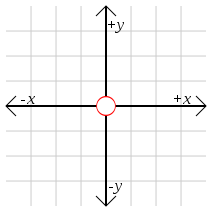
2d cartesian system	2d origin	3d cartesian system
general representation for point a

Several different 2d geometric shapes exist:

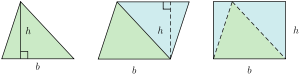
most common 2d shapes. a shape is a polygon, and can have any positive integer number of sides greater than 2

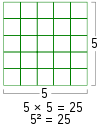
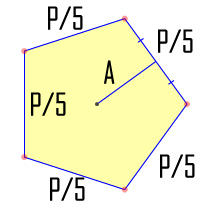
triangle area is b*h/2 square area is length*width polygon area is P*A/2

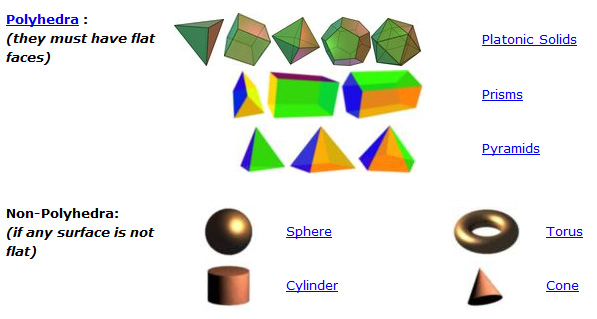
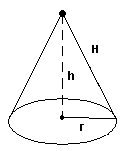
Several different 3d geometric solids exist:

most common 3d solids

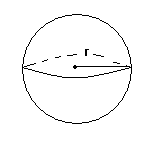
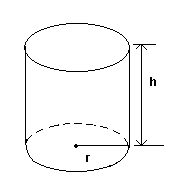
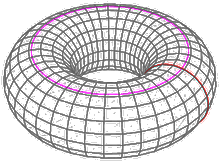
sphere area is 4*3.1415*r^2; cylinder area is 2*3.1415*radius*height torus area is 4*3.1415^2*(pink radius)*(red radius) cone area is 3.1415*r*(r^2+h^2)^.5

In order to understand more specific constructs, a more firm grasp of algebra is required. All numbers can be represented by variables, which can then have basic operations thereof including (but not limited to): adding, subtracting, multiplying, dividing, exponential and parenthesis all of which have applicable processing rules. The most important rule is the order of operations, which states the operations must be performed in this order from first to last:

1. parenthesis
2. exponential
3. multiply
4. divide
5. add
6. subtract

which may be remembered with the mnemonic "PEMDAS".

mathematical truth demonstrating MDAS from above, using integer substitution to start

algebraic truths

algebraic fractional truth

algebraic exponential truths

A function is a mathematical variable output set, each value for which is determined by a variable input:

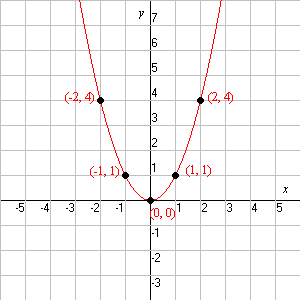
function for a parabola	plot of a parabola
other parabolic functions / plots
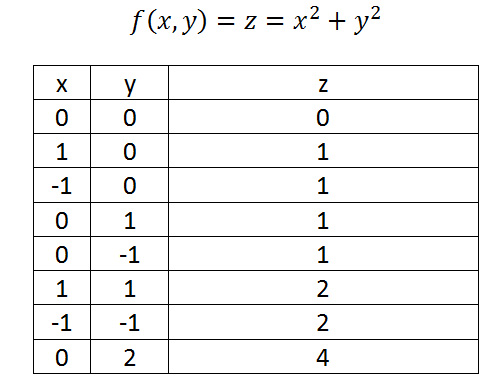
img src="img/learn3d/x2y2.gif" alt="paraboloid"/> plot of a paraboloid	function outputs for the paraboloid equation; the numbers indicate a similarity to a parabola output
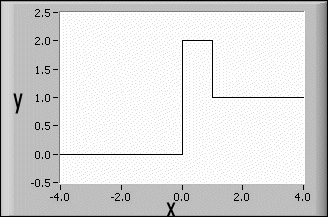
plot of a step function	description of the step function