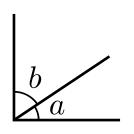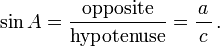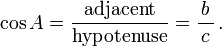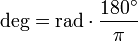Learn 3D Menu
Trigonometry
Trigonometry is useful in determining linear lengths / oscillation with respect to digital art.
Artists traditionally use angles to measure rotations:
|
an angle θ |
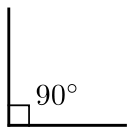
right angle
The complementary angles a and b (b is the complement of a, and a is the complement of b)
Acute (a), obtuse (b), and straight (c) angles. Here, a and b are supplementary angles |
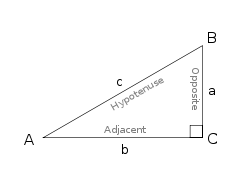
Given a triangle, trigonometry can be used to determine angles and side lengths if some information is known:
|
reference triangle with marked angles, sides and terms |
sine function
cosine function
tangent function these can be memorized using the mnemonic soh-cah-toa |
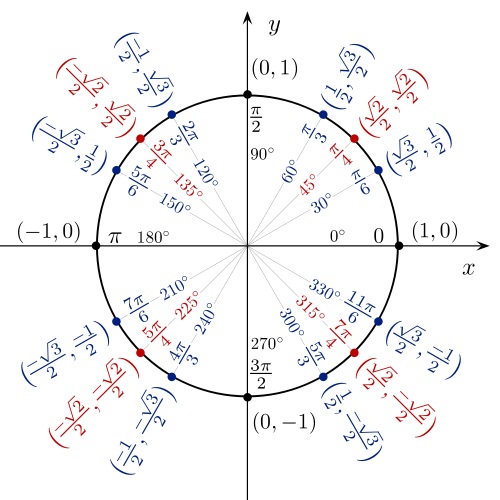
We can make use of radians and advanced trig functions as well:
|
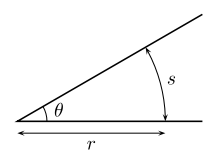
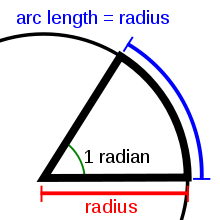
graphical representation of a radian
formula to convert radians to degrees. radians should be converted to degrees once calculations are done because degrees are more familiar to us |
radian plot in common degree increments |
|
introduction of secant, cosecant, and cotangent |
Given these formulas we can solve for the variables:
|
calculation of a tangent angle using the formula and converting from radians |
Oscillation can be represented with sine and cosine curves once plotted:
|
sine and cosine curve |